原创改进直接用！｜多策略改进的白鲸优化器(MSBWO),含函数测试，工程设计问题，消融实验MATLAB

文章来源于我的个人公众号：KAU的云实验台，主要更新智能优化算法的原理、应用、改进
函数测试：

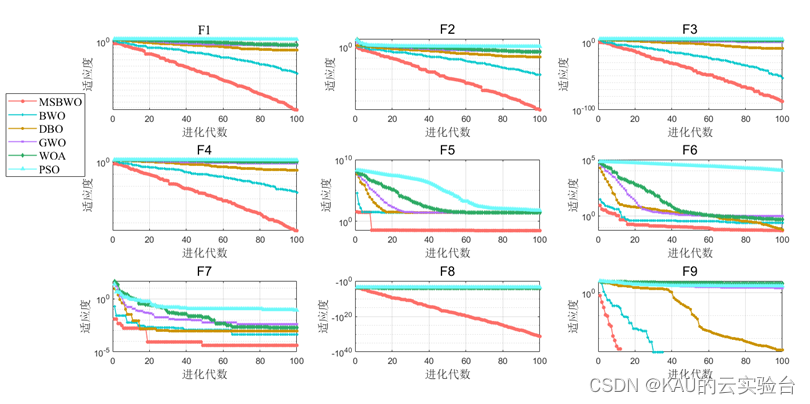
前面的文章中KAU介绍了2022年发表在中科院1区期刊KBS上的优化算法——白鲸优化算法(Beluga Whale Optimization，BWO)[1]，该算法与15种优化算法在30个基准函数和4个真实优化问题上进行测试，均显示出其惊艳的性能。但BWO也和其他算法一样，在某些复杂场景（可以结合你们的应用场景进行描述）中存在收敛速度慢、全局探索能力不足、易陷入局部最优的问题。

因此本文针对BWO提出4点改进，并将其应用于函数测试、工程设计问题测试，与GWO、DBO等算法进行对比实验以验证改进算法的优越性。此外，本文还进行了消融实验，以进一步验证改进策略的有效性。

注：本文所作工作为纯原创

消融实验：

?

工程设计：

1 白鲸优化 (BWO) 算法原理

2 融合多策略改进的白鲸优化算法(MSBWO)

3 代码目录

4 算法性能

5 源码获取

下面简单回顾一下其流程：

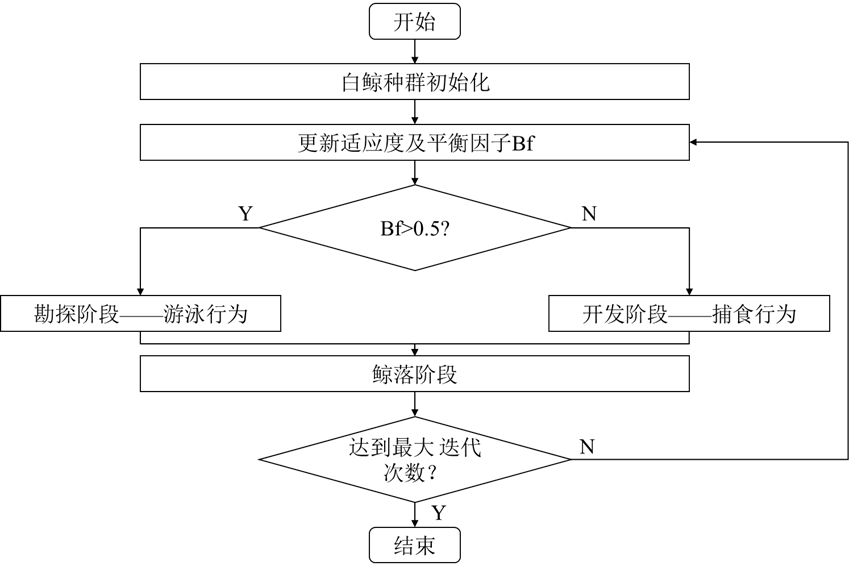
具体原理不再赘述，感兴趣朋友的可以查看往期文章

2.1 初始化种群的改进

2.1.1 初始种群多样化

BWO采用随机生成初始种群的方法，容易出现种群分布不均匀，会导致种群多样性减少，种群质量不高，影响算法的收敛速度。

而混沌映射具有随机性、非重复性和混沌遍历性等特点[2]，意味着它比依赖于概率的随机生成更能够使种群分布均匀。因此，可以利用混沌映射生成初始种群来增加潜在解的多样性。目前文献中常用的混沌映射有Logistic映射、Tent映射和Circle混沌映射等，而Circle映射更为稳定且其混沌值覆盖率高[3]，同时考虑到Circle映射在[0.2,0.6]之间取值较为密集，因此对Circle映射公式进行改进[4]，使其更加均匀。

原 Circle 混沌映射表达式为：

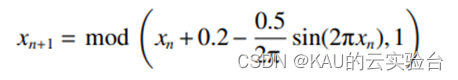
改进后的 Circle 混沌映射表达式为

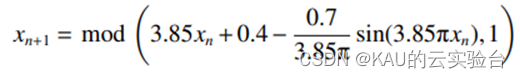
分别用随机初始化、Circle映射、改进的Circle映射作出其分布图：

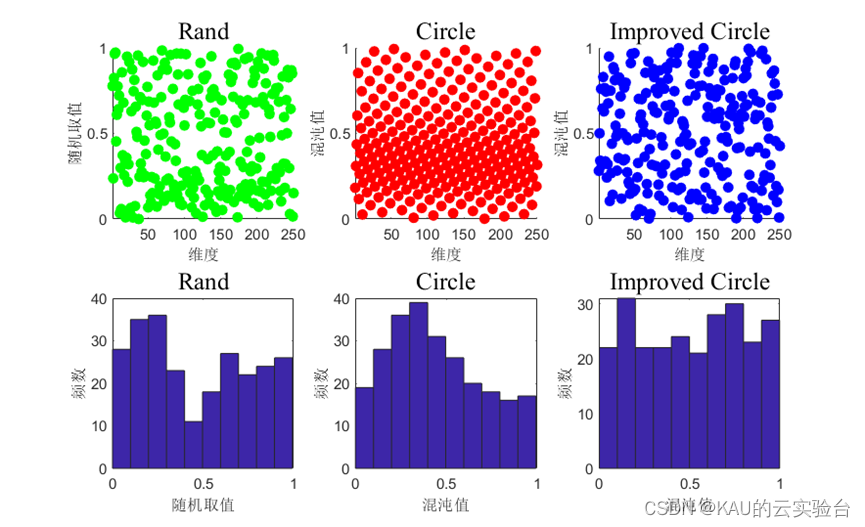
由图可知，改进后的Circle映射在分布的均匀性上有很大提升，能够应用于初始化策略以改善种群的多样性，加强算法的全局搜索能力。

2.1.2 初始种群精英化

反向学习策略是由TIZHOOSH于2005年提出[5]，在当前个体区域内生成相反个体，对比选取适应度高的个体进行后续迭代，可以有效提高种群的质量及多样性，加强算法的搜索能力。

然而，反向学习策略产生的反向解与当前解的距离值固定，缺乏一定的随机性，可能导致搜索空间内的种群多样性无法有效增加，因此本文采用动态反向学习策略来进一步增加算法种群的多样性和种群精英个体的数量[6]，帮助算法扩大搜索区域，从而提高选取更优解的概率。

2.2 精英池策略[7]

BW在进行位置更新时，总是使用当前最优个体作为食物源，若食物源已陷入局部最优，则后续所有个体都将聚拢于局部最优个体，从而导致算法早熟收敛。为增强种群多样性，GWO算法提出了等级制度，将当前最佳的三个头狼的算术平均作为最优位置，以此避免使用一个最优个体引导带来的缺陷。

因此，受GWO的启发，本文引入精英池策略，将当前最优的前3个个体以及3个个体的加权平均作为精英池中的候选精英，在进行位置更新时将随机从精英池中选择一个个体作为引导，以提高算法跳出局部最优的能力。

[图源文献：透镜成像反向学习的精英池侏儒猫鼬优化算法]

2.3 融合自适应Lvey飞行与螺旋搜索的开发阶段

首先，原始BWO的开发阶段采用了固定步长的Levy飞行用以提高其收敛能力，然而，在算法的不同阶段，其期望的Levy飞行的步长可能会有所不同。Levy飞行的步长α越大，越容易搜索到全局最优解，但降低了搜索精度；α越小，搜索精度越高，但降低了搜索速度。（下式中0.01则是其步长）

因此，为增强算法对解空间的探索能力，改善其收敛精度，本文采用自适应的Levy步长策略，在迭代前期Levy飞行具有较大步长，能够充分对解空间进行广度上的探索，而迭代后期Levy飞行步长递减，转而进行更为精细的探索。（图中T即为最大迭代次数）

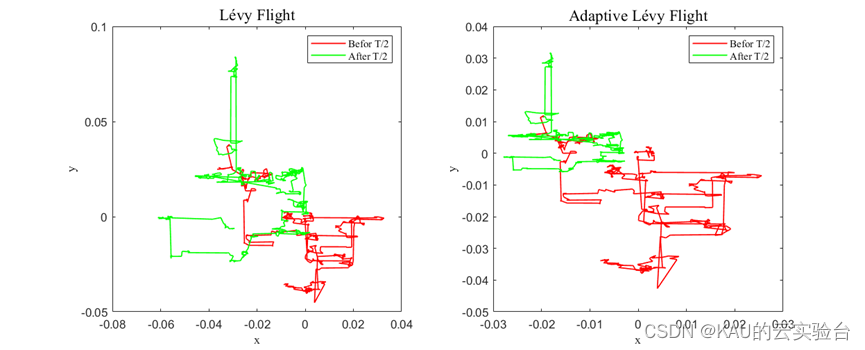
其次，由BWO的开发阶段的位置更新公式可知，其虽涉及随机个体、最佳个体、当前个体，但其对解空间的探索仍可能存在遗漏。鲸鱼优化算法中，鲸鱼个体在搜寻猎物的时候，会根据目标位置（即最优位置）与自身位置之间的螺旋形状调整每次位置更新的移动距离，这种策略能够极大程度上利用区域信息，提高搜索能力，因此本文将该策略引入，以提高算法对局部空间开发的严密性与准确性，增强局部搜索能力。

2.4 黄金正弦策略

黄金正弦算法（Golden Sine Algorithm，Golden-SA）是Tanyildizi等人于2017年提出的一种新型元启发式算法[8]，其依据正弦函数与单位圆的关系，可以遍历正弦函数上的所有点即单位圆上的所有点，算法具有较强的全局搜索能力，且Golden-SA在其位置更新过程中引入了黄金分割数系数，使得算法在每次迭代过程中都会对能产生优秀解的区域进行充分搜索，从而加快了算法的收敛速度，跳出局部最优。

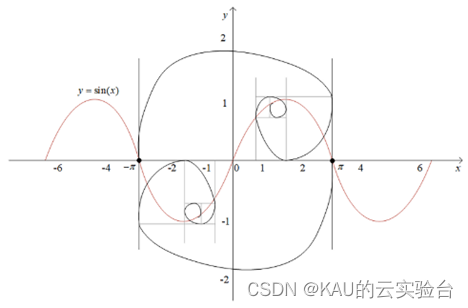
[图源：An improved Harris Hawk algorithm based on Golden Sine mechanism]

因此本文利用黄金正弦策略对BW种群进行更新，以增强BWO的全局搜索能力，加快算法的收敛速度。

2.5 算法流程

代码都为MATLAB编写，在Readme文件中对各文件夹内容作了说明：

代码都经过作者重新注释，代码更清爽，可读性强。

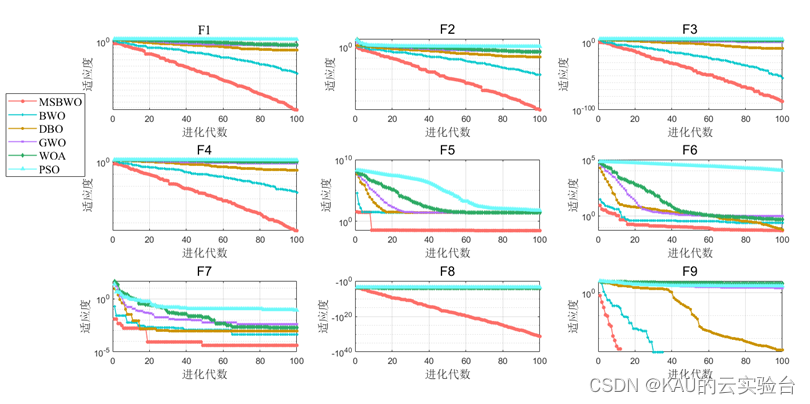
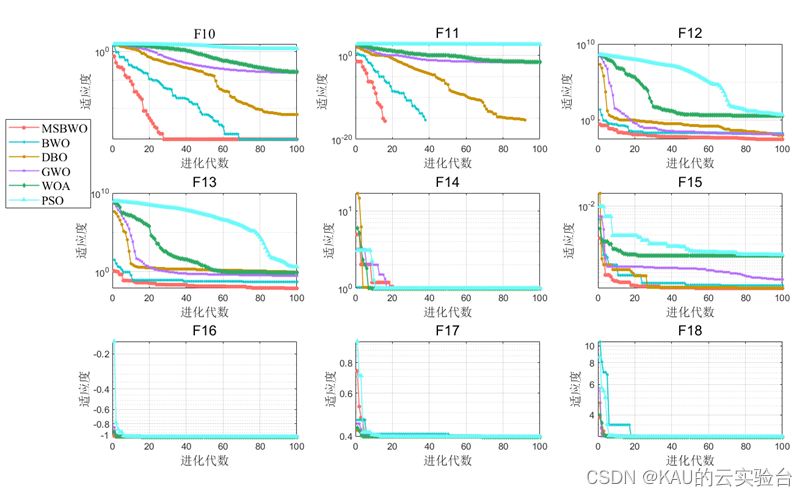
4.1 函数测试

采用CEC2005测试函数检验改进的白鲸优化算法性能。

迭代曲线

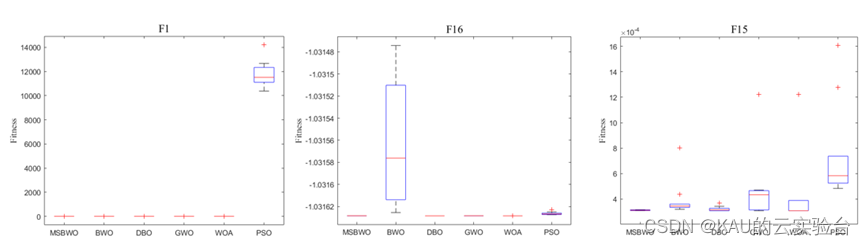
箱型图（展示部分）

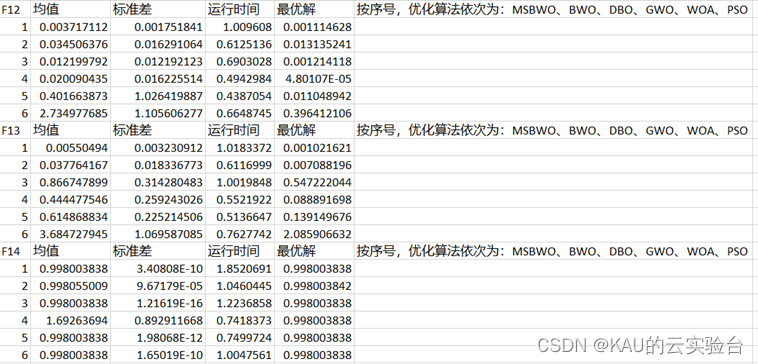
Excel数据文件

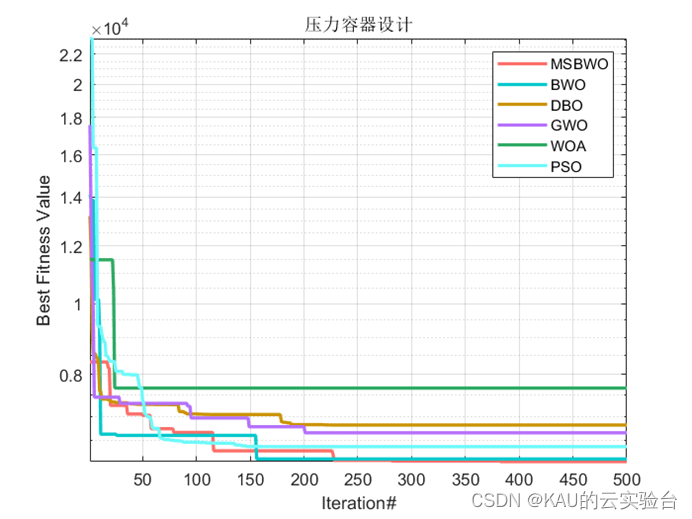
4.2 工程设计问题

对于工程设计问题，通常采用罚函数处理不符合约束的解，本文针对工业制冷系统的优化设计和压力容器设计进行测试，具体数学模型在代码文件中以PDF形式给出，这里不再赘述。

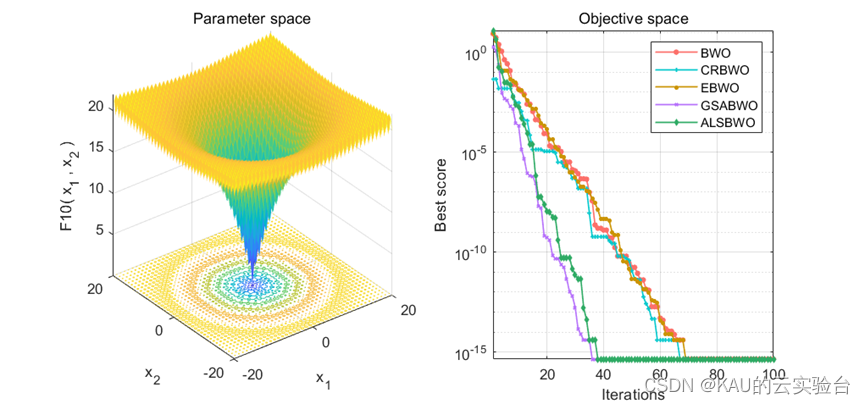
4.3 消融实验

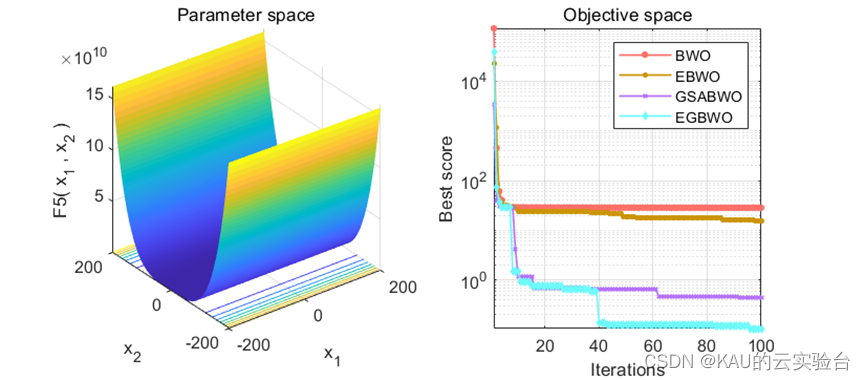
为验证各改进策略对MSBWO的贡献，本文分别将原BWO算法与4种不完全的MSBWO算法进行对比，分别是混沌反向学习BWO(CRBWO)、精英池BWO(EBWO)、自适应Levy螺旋BWO(ALSBWO)和黄金正弦BWO(GSABWO)。

结果如下：

可以看到，改进策略对于原BWO都具有一定的正向作用，观察到精英池策略对BWO影响不大，这是因为精英池策略可以与其他策略（如黄金正弦）协同作用，进一步提升性能，如下：

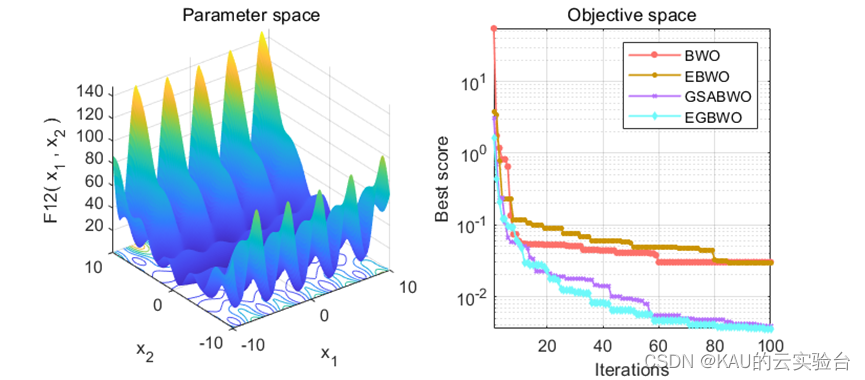
在公众号（KAU的云实验台）后台回复 MSBWO

含完整公式及原理?

除以上改进方法外，针对复杂多峰问题，改进平衡因子以及勘探阶段，提高其前期的全局搜索能力也是可以考虑的方法。

[1] Zhong Changting, Li Gang, Meng Zeng. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm [J]. Knowledge-Based Systems, 2022, 251.

[2] Shi X,Li M. Whale Optimization Algorithm Improved Effectiveness Analysis Based on Compound Chaos Optimization Strategy and Dynamic Optimization Parameters [c]//2019 International Conference on Virtual Reality and Intelligent Systems( ICVRIS) . 2019:123-126.

[3]ZHANG D M, XU H, WANG Y R, et al. Whale optimization algorithm for embedded Circle mapping and onedimensional oppositional learning based small hole imaging[J]. Control and Decision, 2021, 36(5): 1173-1180（in Chinese）.

[4] 宋立钦,陈文杰,陈伟海等.基于混合策略的麻雀搜索算法改进及应用[J].北京航空航天大学学报,2023,49(8):2187-2199.

[5] TIZHOOSH H R. Opposition-based Learning: A New Scheme for Machine Intelligence[C]//IEEE. Proceedings of Computational Intelligence for Modelling, November 28-30, 2005, Vienna, Austria. New York: IEEE, 2005: 695-701.

[6] Yan Ai-jun, Hu Kai-cheng. Improved strategy and its application to the Optimization of seagull optimization algorithm[J]. Information and Control, 2022, 51(6): 688-698.

[7] 汤安迪，韩统，徐登武，等.使用高斯分布估计策略的改进樽海鞘群算法[J].系统工程与电子技术，2022，44（7）：2229-2240.

[8] TANYILDIZI E，DEMIR G.Golden sine algorithm：a novel math-inspired algorithm[J].Advances in Electrical &Computer Engineering，2017，17（2）：71-78.

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞/在看(? _)?(不点也行)，你们的鼓励就是我坚持的动力！若有定制需求，可私信作者。